(M)ein spezielles Aufgabenformat
Die SENSEI-Aufgaben ...
... sind entstanden, um in Klassenarbeiten und Tests ein -auch für die Schüler_innen offensichtliches- einheitliches Format mit Wiedererkennungswert für Aufgaben, die sich im Anforderungsbereich III befinden, zu schaffen. Ein fiktiver Dialog zwischen dem SENSEI und SCHÜLER_IN beginnt stets mit der Frage "Was behandelt ihr gerade im schönen Fach Mathematik?" und endet nach einer Erörterung des Themas mit "Nun, genau das ist heute meine Frage an dich!".
Ihre erfolgreiche Bearbeitung erfordert sowohl eine tiefe inhaltliche Durchdringung des behandelten Stoffes als auch Problemlöse- und Argumentationskompetenz. Zudem verlangt die Dialogform (rezeptive) Kommunikationskompetenz, die sich insofern auszahlt, als Lösungsansätze oft implizit versteckt angegeben sind.
Die folgenden Aufgaben wurden (ggf. für die Website leicht redaktionell bearbeitet) genau so in Klassenarbeiten und Tests ab Schulfahr 1917/18 (für gute Schüler_innen erfolgreich und Freude am Bearbeiten!) gestellt.
Im Zuge des digitalisierten Unterrichts in Corona-Zeiten gibt es kleine Probleme im gleichen Format, die nicht in Arbeiten, sondern online unter dem Titel "Gruß vom SENSEI" veröffentlicht wurden.
Selbstverständlich dürfen diese Aufgaben und dieses Aufgabenformet in Arbeiten,Tests usw. von jedem beliebig bentzt, abgeändert und verbessert werden. Ein Hinweis auf den Ursprung von meiner Website würde mich natürlich freuen, ist aber nicht zwigend notwendig.
Klasse 6/1 : Unterproportionale Zuordnungen untersuchen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben uns mit proportionalen Zuordnungen beschäftigt. |
SENSEI: | Dann weißt du sicherlich, woran man eine proportionale Zuordnung erkennt? |
SCHÜLER: | Klar, wenn die eine der beiden Größen größer wird, dann wird auch die andere größer. |
SENSEI: | Naja, das stimmt zwar, reicht aber nicht aus. Das habt ihr doch bestimmt anders gelernt. |
SCHÜLER: | Ach ja, ich erinnere mich: Wenn die eine der beiden Größen verdoppelt wird, dann verdoppelt sich auch die andere! |
SENSEI: | Genau. Es könnte ja nämlich auch so sein, dass bei Verdoppelung der ersten Größe die zweite zwar auch größer wird, aber weniger als doppelt so groß! Das nennt der Mathematiker dann unterproportionale Zuordnung. |
SCHÜLER: | Gibt es denn sowas?… |
SENSEI: | Klar, denk doch mal daran, dass alle Kinder, wenn sie älter werden, immer weiter wachsen… |
SCHÜLER: | Und was wäre ein Beispiel dafür? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erstelle eine Tabelle, die zu einer unterproportionalen Zuordnung gehören könnte.
(2) Zeichne im vorgegebenen Koordinatensystem ein, wie die graphische Darstellung einer unterproportionalen Zuordnung aussehen könnte!
Klasse 7/1 : Unterproportionale Zuordnungen untersuchen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben uns mit proportionalen und antiproportionalen Zuordnungen beschäftigt. |
SENSEI: | Dann weißt du sicherlich, wie eine proportionale Zuordnung definiert ist? |
SCHÜLER: | Klar, wenn die eine der beiden Größen größer wird, dann wird auch die andere größer. |
SENSEI: | Naja, das stimmt zwar, reicht aber als präzise Definition nicht aus, wie du sicher weißt. Das habt ihr auch bestimmt anders gelernt. |
SCHÜLER: | Ach ja, wenn die eine der beiden Größen verdoppelt wird, dann ver-doppelt sich auch die andere! |
SENSEI: | Genau. Es könnte doch nämlich auch so sein, dass bei der Verdoppelung der ersten Größe die zweite Größe zwar auch größer wird, aber weniger als doppelt so groß wird! |
SCHÜLER: | Gibt es denn sowas?… |
SENSEI: | Klar, solche Zuordnungen haben sogar einen Namen, sie heißen „unterproportional“! |
SCHÜLER: | Und was wäre ein Beispiel dafür? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Gib ein Beispiel für eine unterproportionale Zuordnung an (z.B. durch Angabe der Größen oder eine Aufgabenstellung) und begründe kurz die Richtigkeit deines Beispiels.
(2) Zeichne in ein Koordinatensystem ein, wie der Graph einer unterproportionalen Zuordnung aussehen könnte!
Klasse 7/2 : Mit Prozenten rechnen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben uns ganz lange mit Prozentrechnung beschäftigt. |
SENSEI: | Das ist gut und zudem sehr wichtig, weil man im Leben oft mit Prozentzahlen konfrontiert wird. |
SCHÜLER: | Ja, so ging es mir gestern. Da habe ich im Laden eines Freundes ein T-Shirt gesehen, an dem stand „Preisermäßigung um 20%“. Klingt gut, oder? |
SENSEI: | Durchaus, das wäre ein tolles Schnäppchen. Hast du dann das Shirt gekauft? |
SCHÜLER: | Nein, natürlich nicht! Ich habe nämlich von meinem Freund erfahren, dass seine Eltern im Geschäft vor der Preisreduzierung das Shirt um genau 20% verteuert haben! |
SENSEI: | Das ist ja irgendwie fast Betrug! |
SCHÜLER: | Genau! Erst 20% teurer und dann 20% billiger – so ein Quatsch! |
SENSEI: | Wäre aber trotzdem ein -zugegeben kleineres- Schnäppchen für dich gewesen! |
SCHÜLER: | Wieso denn das? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erläutere, warum die Rechnung des Verkäufers nicht aufgeht!
(2) Berechne, wie groß wäre das "Schnäppchen" gewesen wäre.
Klasse 7/3 : Zahlen unterschiedlich darstellen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir beschäftigen und damit, wie man Zahlen darstellen kann. |
SENSEI: | Und was fällt die dazu ein? |
SCHÜLER: | Naja, die "zwölf" z.B. kann ich durch 12 Striche, römisch als XII, als Bruch als 24/2, als Dezimalzahl als 12,000 darstellen, oder aber im Stellenwertsystem als einen Zehner plus zwei Einer ... also 12. |
SENSEI: | Ja, das Stellenwertsystem ist schon eine gute Erfindung. Im Dezimalsystem werden ja immer zehn Einheiten zu einer größeren Einheit zusammengefasst: Zehn Einer sind ein Zehner, zehn Zehner ein Hunderter, zehn Hunderter ein Tausender usw. |
SCHÜLER: | Klar, das ist doch Stoff der Grundschule, das kann ich problemlos! |
SENSEI: | Wie wäre es aber, wenn ich nicht immer zehn Einheiten zu einer neuen Einheit zusammenfasse, sondern nur jeweils zwei? Der Mathematiker nennt das dann Dualsystem! |
SCHÜLER: | Wie soll denn das gehen? |
SENSEI: | Nun, dann gibt es nur null oder einen Einer, weil zwei Einheiten sind dann ja schon ein Zweier, zwei Zweier ein Vierer, zwei Vierer ein Achter usw. Zwölf wäre dann ein Achter, ein Vierer, kein Zweier, kein Einer und würde 1100 geschrieben. |
SCHÜLER: | Aber warum macht man den so etwas? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Gib an und erkläre, wie die Dezimalzahl 19 als Dualzahl geschrieben wird.
(2) Gib je einen Vorteil und einen Nachteil an, eine Zahl als Dualzahl zu schreiben
(3) Erörtere den Ausspruch "Es gibt genau 10 Positionen zum Dualsystem: Entweder man versteht es, oder man versteht es nicht".
Klasse 7/4 : Mit ganzen Zahlen rechnen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir beschäftigen uns schon ganz lange mit den ganzen Zahlen. |
SENSEI: | Dann weißt du sicherlich, wie ganze Zahlen addiert und subtrahiert werden? |
SCHÜLER: | Klar, da gibt es Regeln, die haben wir erarbeitet und aufgeschrieben. |
SENSEI: | Aber was ist mit der Multiplikation? Kannst du auch schon ganze Zahlen miteinander multiplizieren? |
SCHÜLER: | Nein, wie soll das denn gehen? Was soll denn z.B. (+3) mal (-2) sein? |
SENSEI: | Na dann rechne doch erst einmal 3 mal 102 aus! |
SCHÜLER: | Was hat das denn damit zu tun? |
SENSEI: | Sehr guter Trick! Der Mathematiker nennt deinen Trick „Distributivgesetz“. Und das kann dir auch helfen zu erklären, was (+3) mal (-2) sein muss, wenn es weiterhin gelten soll! |
SCHÜLER: | Klar soll alles, was bislang galt, auch weiterhin gelten. Unser Lehrer hat das als das „Mathematisches Permanenzprinzip“ bezeichnet. |
SENSEI: | Ja, das stimmt. Na dann bestimme damit mal, was (+3) mal (-2) sein muss, denn genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Erkläre an dieser Aufgabe, welcher Wert für (+3) mal (-2) sinnvoll ist!
(2) Gib kurz an, wie man mit dem gleichen Verfahren auch den Wert von (-3) mal (-2) bestimmen kann!
Klasse 7/5 : Die merkwürdige Zahl "i" untersuchen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben jetzt die rationalen Zahlen kennengelernt und rechnen damit! |
SENSEI: | Dann weißt du sicher auch, wozu man rationale Zahlen braucht? |
SCHÜLER: | Klar, in den natürlichen Zahlen, den ganzen Zahlen und den Bruchzahlen gibt es immer wieder Aufgaben, die noch nicht rechenbar sind. Und um auch das zu können definieren wir neue, weitere Zahlen. |
SENSEI: | Und du meinst, in den rationalen Zahlen kann man jetzt jede Aufgabe rechnen? |
SCHÜLER: | Klar, welche Aufgabe denn nicht, mal abgesehen von der unsinnigen und verbotenen Division durch null? |
SENSEI: | Na dann nenne mir doch einmal die Zahl, die mit sich selbst malgenommen -1 ergibt! |
SCHÜLER: | Stimmt, das geht nicht! |
SENSEI: | Natürlich nicht, und genau deswegen definieren Mathematiker eine solche Zahl, mit der das geht, und nennen sie einfach „ i “. |
SCHÜLER: | Also dann ist i ∙ i = -1 ? |
SENSEI: | Genau! Und wie man sonst noch mit dieser merkwürdigen Zahl rechnet, das ist heute meine Frage an dich … |
Aufgaben:
(1) Erkläre, warum es in den rationalen Zahlen keine Zahl geben kann, die mit sich selbst malgenommen -1 ergibt.
(2) Berechne i ∙ [ i + i ] !
(3) Untersuche was passiert, wenn i genau 41 mal mit sich selbst malgenommen wird!
Klasse 7/6 "Gruß vom SENSEI 1" : Addition und Multiplikation von Variablen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben haben gelernt, was Terme sind und wie man sie einfacher schreiben kann! |
SENSEI: | Dann weißt du sicherlich den Unterschied zwischen "2 mal x" und "x hoch 2"? |
SCHÜLER: | Klar, das erste ist eine Kurzschreibweise für "x plus x" und das andere für "x mal x" ... und das ist ja wohl was anderes! |
SENSEI: | Das stimmt natürlich grundsätzlich ... Wenn du für x den Wert 10 einsetzt, dann hat der erste Term den Wert 20 und der zweite Term aber den Wert 100. Aber das ist nicht immer bei allen Zahlen so! |
SCHÜLER: | Wieso? Gibt es denn Zahlen, für die beide Terme den gleichen Wert haben? |
SENSEI: | Ja, sogar mehrere, und welche das sind, das ist heute meine Frage an dich. |
Aufgabe:
(1) Gib an, um welche Zahlen es sich handelt.
Klasse 7/7 "Gruß vom SENSEI 2" : Lösbarkeit von Gleichungen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Nach den Termen und Termumformungen haben wir nun gelernt, was Gleichungen sind und auch, wie man sie lösen kann. |
SENSEI: | Dann kannst du ja sicherlich die Gleichung "x hoch 2 gleich 2,25" lösen? |
SCHÜLER: | Klar doch, "x hoch 2" heißt ja nichts weiter als "x mal x". Aber zur Sicherheit möchte ich doch noch einmal Nora und Ali fragen, die sind noch besser als ich in Mathe. |
später... | |
SENSEI: | Und? Zu welchem Ergebnis seid ihr gekommen? |
SCHÜLER: | Da haben wir jetzt ein Problem. Ich meine die Gleichung hat genau zwei Lösungen, nämlich 1,5 und -1,5, da dann ja immer, wenn man es miteinander multipliziert, genau 2,25 herauskommt. Nora aber meint, nur 1,5 sei die einzige Lösung. Und Ali behauptet sogar, dass die Gleichung unlösbar sei! |
SENSEI: | Und wie, wenn ihr vielleicht alle drei, jeder auf seine Weise, recht hättet? |
SCHÜLER | Aber wie soll denn das gehen? |
SENSEI: | Genau das ist heute meine Frage an euch! |
Aufgaben:
(1) Erkläre, warum alle drei recht haben können!
(2) Erkläre, warum auch Jean mit der Behauptung, die Gleichung sei allgemeingültig, recht haben kann!
Klasse 8/1 : Binomische Formeln hinterfragen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben uns mit den binomischen Formeln beschäftigt, ist total easy … |
SENSEI: | Dann kannst du mir sicherlich die erste und zweite binomische Formel auswendig sagen? |
SCHÜLER: | Klar, das habe ich gelernt, sind ja einfach zu merkende Formeln: a plus b in Klammern zum Quadrat ist gleich a zum Quadrat plus b zum Quadrat plus zwei mal a mal b. Bei der zweiten binomischen Formel ändern sich nur Vorzeichen |
SENSEI: | Aber warum musst du dir hier zwei Formeln merken, das ist doch nicht effizient, eine Formel reicht nämlich! |
SCHÜLER: | Wieso? Die eine Formel ist mit „+“ und die andere mit “-“, ist doch was total anderes … |
SENSEI: | Naja, eigentlich nicht. Erinnerst du dich nicht daran, wie wir uns damals über negative Zahlen unterhalten haben? |
SCHÜLER: | Ja, schon. Aber was hat das damit zu tun? |
SENSEI: | Genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Begründe, warum die erste und zweite binomische Formel eigentlich nicht unterschieden werden müssten und somit die zweite binomische Formel ersetzbar ist.
(2) Gib an, warum die dritte binomische Formel nicht ersetzbar ist.
Klasse 8/2 : Potenzen mi dem Exponenten null
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben uns mit Potenzen beschäftigt, das ist eine Schreibweise, wenn man eine Zahl ganz oft nit sich selbst malnimmt. |
SENSEI: | Genau. Dann kannst du mir bestimmt sagen, was 2 hoch 3 ist. |
SCHÜLER: | Na klar, das ist zwei mal zwei mal zwei, also acht! |
SENSEI: | Und was ist zwei hoch drei mal zwei hoch vier? |
SCHÜLER: | Das ist auch ganz einfach, ich hab da einen Trick: Ich zähle einfach drei und vier zusammen und habe dann das Ergebnis zwei hoch sieben. |
SENSEI: | Das stimmt, ist aber nicht nur ein "Trick", sondern sogar ein mathematisches Gesetz, Mathematiker nennen es das "1. Potenzgesetz". |
SCHÜLER: | Potenzen sind ja soooo einfach... |
SENSEI: | Na dann kannst du mir sicherlich auch erklären, was zwei hoch null ist? |
SCHÜLER: | Äh? Wie soll denn das gehen? Das ist doch Unsinn. Ich schreibe keine zwei hin? Dann kann ich ja auch nichts miteinander malnehmen! |
SENSEI: | Das stimmt. Zwei hoch null muss also anders definiert werden. Mathematiker machen das so, dass auch mit der neuen Definition alle bisherigen Gesetze weiterhin gelten, sie nennen das das "Mathematische Permanenzprinzip". |
SCHÜLER: | Ja, aber was soll denn dann zwei hoch null sein? |
SENSEI: | Genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Gib an und erkläre, wie zwei hoch null definiert werden muss, damit das Mathematische Permanenzprinzip eingehalten werden kann.
(2) Gib ohne Begründung an, wie dementsprechend zwei hoch minus eins definiert werden müsste.
Klasse 8/3 : Rechteckverdoppelung
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben einen Text von Platon gelesen, in dem er einem Jungen beweist, dass man ein doppelt so großes Quadrat bekommt, wenn man als Grundseite die Diagonale des Ausgangsquadrates nimmt. |
SENSEI: | Ja, aber wie lang ist denn nun die Diagonale in einem Quadrat? |
SCHÜLER: | Naja, wenn die Grundseite die Länge 1 hat, dann ist die Länge der Diagonalen √2, das kann ich sogar mit dem Satz des Pythagoras beweisen! |
SENSEI: | Für ein Quadrat mit den Seitenlänge a=1 ist das richtig. Aber wie ist das in einem Quadrat mit einer beliebigen Seitenlänge a? |
SCHÜLER: | Ohje, da muss ich mal etwas überlegen, … |
SCHÜLER überlegt und kritzelt was auf seinen Notizblock.
SCHÜLER: | Das ist ja auch √2, nur noch malgenommen mit der Seitenlänge a! |
SENSEI: | Auch das stimmt. Nun kannst du mir sicher auch sagen, wie lang die Seiten eines Rechtecks sein müssen, das genauso aussieht wie das Ausgangsrechteck, aber den doppeelten Flächeninhalt hat? |
SCHÜLER: | Äh? Da hilft mir aber die Diagonale doch nicht, damit bekomme ich doch kein Rechteck, sondern nur ein Quadrat. |
SENSEI: | Das stimmt, die Diagonale hilft da wirklich nicht, aber √2, die auch hier eine ganz wichtige Rolle spielt. |
SCHÜLER: | Ja...aber wie denn? |
SENSEI: | Genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Bestätige unter Benutzung einer kurzen, kommentierten Rechnung, dass das flächenmäßig doppelt so große Quadrat zu einem gegebenen Quadrat mit der Grundseitenlänge a als Grundseitenlänge √2∙a hat.
(2) Untersuche, ob bzw. wie diese Erkenntnis zu einer Vermutung führen kann, wie die Seitenlangen eines Rechtecks sich verändern müssen, um ein doppelt so großes, aber „gleich aussehendes“ Rechteck zu erhalten.
(3) Beweise die Richtigkeit deiner Vermutung.
Klasse 8/4 : Beweis des Satzes von Pythagoras
SENSEI: | Was behandelt ihr gerade im schönen Fach Matrhemaik? |
SCHÜLER: | Wir haben den Satz von Pythagoras gelernt: a zum Quadrat plus b zum Quadrat ist gleich c zum Quadrat! Und das gilt immer... haben sogar schon die alten Ägypter gewusst und angewendet... |
SENSEI: | Ja, aber gilt denn das in dieser Form und mit diesen Bezeichnungen so immer? |
SCHÜLER: | Nein, natürlich müssen wir ein rechtwinkliges Dreieck haben, in dem a und b Katheten sind und c die Hypotenuse ist. |
SENSEI: | Das ist richtig und wichtig. Aber woher weißt du eigentlich, ob der Satz von Pythagoras auch wirklich stimmt? |
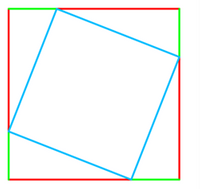
SCHÜLER: | Das haben wir im Unterricht bewiesen, dazu haben wir Dreiecke und Quadrate gezeichnet. Schau mal … |
(zeigt dem SENSEI diese Skizze)
SCHÜLER: | Das haben wir gezeichnet, und dann haben wir Flächeninhalte verglichen und mit den binomischen Formeln gerechnet …. habe ich aber nicht so ganz verstanden. |
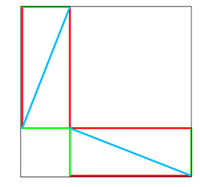
SENSEI: | Das ist auch nicht einfach, aber der Beweis geht mit dieser Skizze auch ganz leicht, ohne komplizierte Rechnung, Gleichungen und binomische Formeln. Sieh dir einfach mal hier meine zweite Skizze dazu an! |
(zeigt dem SCHÜLER seine Skizze)
SENSEI: | Das ist auch nicht einfach, aber der Beweis geht mit dieser Skizze auch ganz leicht, ohne komplizierte Rechnung, Gleichungen und binomische Formeln. Sieh dir einfach mal hier meine zweite Skizze dazu an! |
SCHÜLER: | Äh? Ja, gut, ein weiteres Quadrat, genauso groß wie das in unserer Skizze aus dem Unterricht … aber wie soll ich damit den Pythagoras beweisen? |
SENSEI: | Genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Erkläre in einem zusammenhängenden Text, wie mit Hilfe der obigen Skizzen der Satz von Pythagoras bewiesen werden kann.
Klasse 8/5 : Volumenformeln
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir zeichnen und berechnen alle möglichen Körper, also Würfel, Quader, Prismen, Zylinder, Pyramiden, Kegel, und die Kugel kommt wohl auch noch dran. |
SENSEI: | JDann kannst du mir sicherlich sagen, was alle diese Körper gemeinsam haben und worin sie sich unterscheiden? |
SCHÜLER: | Na klar, sie haben alle eine Oberfläche und ein Volumen, das man berechnen kann. Manche haben eine Grund- und Deckfläche, manche nur eine Grunsfläche und dann eine Spitze, abgesehen von der Kugel, die ist völlig anders. Und deshalb muss man sich so viele verschiedene Formeln merken, aber das fällt mir schwer, ich verwechsele die ganz oft. |
SENSEI: | Aber für die Volumenberechnung musst du dir doch -abgesehen von der Kugel, die ihr ja noch nicht behandelt habt- eigentlich nur zwei noch dazu sehr ähnliche Formeln merken. |
SCHÜLER: | Aber ... Zwei Formeln brauche ich doch schon nur für Würfel und Quader, einmal V=a*a*a und einmal V=a*b*c. Und dann gibt es auch noch Prismen und Zylinder, gerade und schräge Pyramiden, Kegel und und und ... Und alle haben ganz andere Volumenformeln mit verschiedensten Größen. Warum sollen für diese vielen Körper nur zwei Volumenformeln reichen? |
SENSEI: | Genau das ist heute meine Frage an dich … |
Aufgaben:
(1) Begründe, warum es tatsächlich reicht, sich für die Volumenberechnung nur zwei Formeln zu merken.
(2) Erläutere, worin dann aber bei der Benutzung dieser lediglich zwei Formeln häufig die Schwierigkeit besteht.
Klasse 9/1 : Wurzeln als Potenzen schreiben
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir machen was mit Wurzeln! |
SENSEI: | Oh, dann kannst du mir sicher sagen, was die Wurzel aus sechzehn ist? |
SCHÜLER: | Natürlich, das ist vier, weil vier mal vier sechzehn ist. |
SENSEI: | Stimmt genau! Und was ist die vierte Wurzel aus sechzehn? |
SCHÜLER: | Ich glaube, das ist zwei, weil zwei viermal mit sich selbst malgenommen sechzehn ergibt. |
SENSEI: | Auch richtig! Dann kannst du mir sicher auch sagen, was die erste Wurzel aus sechzehn ist, oder? |
SCHÜLER: | Aber Sensei, das macht doch keinen Sinn … eine Zahl zu suchen, die überhaupt nicht mit sich selbst multipliziert wird und dann sechzehn ergibt … |
SENSEI: | Doch, durchaus … wenn sechzehn mit nichts multipliziert wird, dann bleibt es eben sechzehn! |
SCHÜLER: | Also wäre die erste Wurzel aus sechzehn genau sechzehn selbst? |
SENSEI: | Du hast es erfasst. Aber jetzt wird es noch schwieriger. Was wäre denn dann die 0,5te Wurzel aus 16? |
SCHÜLER: | Ja kann man das denn überhaupt sagen? |
SENSEI: | Nun,genau das ist heute meine Frage an dich ... |
Aufgabe:
(1) Gib an und erläutere, welcher Wert für die 0,5te Wurzel aus 16 sinnvoll erscheint!
Klasse 9/2 : Den Tangens als weitere Winkelfunktion definieren
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben gelernt, wie man den Sinus und Cosinus eines Winkels in einem rechtwinkligen Dreieck über die Längen der Katheten und der Hypotenuse berechnet. |
SENSEI: | Aber du kannst sicherlich auch Sinus und Cosinus mit dem Taschenrechner berechnen? |
SCHÜLER: | Na klar, das haben wir auch geübt, gibt dafür Tasten am Taschenrechner. |
SENSEI: | Gut. Dann wirst du jetzt lernen, was der Tangens eines Winkels ist. |
SCHÜLER: | Und was soll das sein? |
SENSEI: | Nun, den Tangens eines Winkels erhältst du, wenn du im rechtwinkligen Dreieck die Länge der Gegenkathete durch die Länge der Ankathete des Winkels teilst. |
SCHÜLER: | Das ist ja einfach, fast genauso wie beim Sinus und Cosinus, nur ohne die Hypotenuse! |
SENSEI: | Ja, sehr einfach. Und auch dafür gibt es eine Taste auf dem Taschenrechner. Aber eigentlich brauchst du die gar nicht, es reichen die Tasten für den Sinus und den Cosinus, damit kannst du auch schon den Tangens berechnen. |
SCHÜLER: | Aber Sensei, was hat denn der Tangens mit Sinus und Cosinus eines Winkels zu tun? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erkläre, wie du den Wert des Tangens eines Winkels mit dem Taschenrechner nur unter Benutzung der Sinus- und Cosinus-Taste berechnen kannst, also ohne die Tangens-Taste zu benutzen.
(2) Gib an, welcher Zusammenhang dir hilft, dass du den Wert des Tangens eines Winkels mit dem Taschenrechner sogar unter Benutzung nur der Sinus-Taste (also auch ohne Cosinus-Taste) berechnen kannst.
Klasse 9/3 : Den trigonometrischen Pythagoras beweisen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir machen Trigonometrie, Winkelfunktionen, Sinus und Kosinus … |
SENSEI: | Dann weißt du bestimmt, dass Sinus und Kosinus miteinander zusammenhängen? |
SCHÜLER: | Na klar, die sind ja beide nur in rechtwinkligen Dreiecken definiert, nur einmal nimmt man die Gegenkathete und das andere Mal die Ankathete, die Hypotenuse kommt immer vor. |
SENSEI: | Dann weißt du sicher auch, dass für jeden beliebigen spitzen Winkel α stets [sin(α)]^2+[cos(α)]^2=1 ist, oder? |
SCHÜLER: | Nein, ist mir neu.Aber irgendwie sieht das aus wie der Satz des Pythagoras, oder? |
SENSEI: | Genau. In jedem rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat. Der eben genannte Zusammenhang heißt deswegen unter Mathematikern auch „Trigonometrischer Pythagoras“. |
SCHÜLER: | Ja, aber warum ist das so? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erstelle eine Skizze, die den Sachverhalt des „Trigonometrischen Pythagoras“ darstellt.
(2) Begründe die Richtigkeit des „Trigonometrischen Pythagoras“, d.h. der Aussage [sin(α)]^2+[cos(α)]^2=1.
Klasse 9/4 : Mit dreidimensionalen Körpern umgehen
Der KÜNSTLER, übrigens ein guter Freund des SENSEI, hat einen quaderförmigen Marmorblock mit den Maßen 0,5x1x2 Metern. Aus diesem Block soll er eine Skulptur als Gedenktafel erstellen. Sein Auftraggeber hat ihm nebenstehende Skizze zur Verfügung gestellt.
Noch ehe der KÜNSTLER mit der mit der Arbeit angefangen hat, kommt zufällig der SENSEI des Weges.
SENSEI: | Hallo, mein Freund, was willst du Schönes aus diesem Marmorblock formen? |
KÜNSTLER: | Einen Gedenkstein. Und so soll der Gedenkstein aussehen: Es ist einenquaderförmiger Marmorblock mit den Maßen 0,5x1x2 Metern.Die Skulptur soll zwei Meter hoch und breiter als tief (nach hinten gehend) sein soll. Der Sockel soll nur im unteren Viertel der Skulptur quaderförmig bleiben. |
KÜNSTLER zeigt SENSEI die Skizze.
SENSEI: | Schön … wenn es dein Auftraggeber so will! Aber ich fände es schöner, wenn der Gedenkstein aus einem Quader mit einer aufgesetzten Viertelkugel bestünde, wobei vorne die glatte Fläche für die Inschrift wäre! |
KÜNSTLER: | Aber geht denn das überhaupt? |
SENSEI: | Du hast Glück, grundsätzlich ja … Aber natürlich nicht, wenn der Sockel so mit den angegebenen Maßen bleiben soll. |
KÜNSTLER: | Aber wie denn dann? |
SENSEI: | Nun, genau das ist die Frage, die dir meine treuen und inzwischen gut im Umgang mit Problemen geübten Schüler sicherlich beantworten können … |
Aufgaben:
(1) Begründe, warum es grundsätzlich möglich ist, im oberen Teil den Marmorblock zu einer Viertelkugel „zurechtzuschneiden“.
(2) Gib an, wie sich dann die Sockelhöhe verändert.
Klasse 10/1 : "Dreimol Null es Null es Null …“ untersuchen - und singen!
Der SENSEI singt fröhlich
SENSEI: | Dreimol Null es Null es Null, denn mer woren en d'r Kayjass en d'r Schu…u…ul … |
SCHÜLER: | Sensei! Was soll das bedeuten? |
SENSEI: | Es ist Karneval, da singt man sowas, zumindest in Köln! Aber ihr seid ja immer so ernst …Also: Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir behandeln Potenzfunktionen … |
SENSEI: | Und welche Zahlen dürfen bei euch als Exponenten auftreten? |
SCHÜLER: | Alle ganzen Zahlen, also 1, -1, 2, -2, 3, -3, 4, -4, und dann immer so weiter … |
SENSEI: | Aber was ist mit der Null? |
SCHÜLER: | Aber Sensei, das ist doch besonders einfach, schließlich ist jede Zahl hoch null immer eins, das haben wir bewiesen! |
SENSEI: | Dreimol Null is Null es Null ... Aber stimmt das auch für null mal die Null, also null hoch null? Denk doch mal an das mathematische Permanenzprinzip! |
SCHÜLER: | Darüber habe ich mir bisher noch keine Gedanken gemacht … |
SENSEI: | Also dann ist es genau jetzt -Karneval hin , Karneval her- an der Zeit, darüber nachzudenken…Und ja, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erläutere, warum 0^0 nicht sinnvoll definiert werden kann.
(1) Erörtere, ob die Potenzfunktion p0 mit p0(x)=x^0 eher den Potenzfunktionen mit positiven oder negativen Exponenten zuzuordnen ist.
Klasse 10/2 : Probleme am Einheitskreis lösen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir beschäftigen uns mit dem Einheitskreis, schon eine lange Zeit… |
SENSEI: | Ja, ja,die Zeit … Mit der Zeit ist es so ein Ding. Siehst du die Uhr dort an dem Turm? |
SCHÜLER: | Na klar, eine ganz normale Uhr mit zwei Zeigern, dem großen Zeiger für die Minuten und dem kleinen Zeiger für die Stunden. |
SENSEI: | Genau. Und weil die Zeit aber nur langsam vergeht, bewegen sich auch die Zeiger sehr langsam… |
SCHÜLER: | Klar, und das immer mit der gleichen Geschwindigkeit, da ja die Zeit immer gleich vergeht, oder? |
SENSEI: | Das schon, aber der große Zeiger -der Minutenzeiger- legt an seiner Spitze ja einen längeren Weg zurück als der kleine Zeiger an seiner Spitze, außerdem läuft der auch so viel langsamer. Und du weißt ja bestimmt, dass Geschwindigkeit der zurückgelegte Weg pro Zeit ist, also die Weglänge geteilt durch die verstrichene Zeit. |
SCHÜLER: | Klar, ich muss einfach den zurückgelegten Weg durch die Zeit teilen, entweder Kilometer pro Stunde oder Meter pro Sekunde. |
SENSEI: | Genau. Übrigens ist der Große Zeiger der Uhr genau ein Meter lang. |
SCHÜLER: | Ja und? |
SENSEI: | Nun, dann solltest du einmal darüber nachdenken, wie schnell sich dieser Zeiger bewegt, denn das ist heute meine Aufgabe für dich … |
Aufgaben:
(1) Begründe, warum es nicht sinnvoll ist, für einen Zeiger einer Uhr von der Geschwindigkeit des Minutenzeigers zu sprechen.
(2) Bestimme, mit welcher Geschwindigkeit (in Meter pro Sekunde) sich die Spitze des Minutenzeigers der Turmuhr bewegt.
Klasse 10/3 Besonderheiten des dekadischen Logarithmus beweisen
SENSEI: | Was be handelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir haben jetzt gelernt, was Logarithmen sind. |
SENSEI: | Dann habt ihr auch bestimmt den dekadischen Logarithmus behandelt? |
SCHÜLER: | Na klar, das ist doch ein ganz einfacher Logarithmus, nämlich der zur Basis 10! |
SENSEI: | Genau. Und die 10 hat ja in unserem Re-chensystem eine sehr wichtige Bedeu-tung, hast du sicher gelernt. |
SCHÜLER: | Klar, das lernt man doch schon in der Grundschule, wir geben alle Zah-len ja mit den Vielfachen von Zehnerpotenzen an. |
SENSEI: | Genau, der Mathematiker nennt das „Stellenwertsystem“. |
SCHÜLER: | Ich erinnere mich … Einer, Zehner, Hunderter, Tausender usw. Aber jetzt sind wir doch bei den Logarithmen, und zum Rechnen nehmen wir den Taschenrechner. |
SENSEI: | Na dann bestimme mir doch mal den Logarithmus von 512 zur Basis 10. |
SCHÜLER berechnet den Wert mit dem Taschenrechner und zeigt ihn dem SENSEI
SENSEI: | Richtig, gut gemacht. Und nun berechne auch mit dem Taschenrechnerden Logarithmus von 5,12 zur Basis 10. Und dann schau einmal, was dabei herauskommt ... |
SCHÜLER: | (erstaunt) Das ist ja ein merkwürdiger Zufall! |
SENSEI: | Nein, das ist es nicht, sondern das muss sogar so sein, und zwar immer! |
SCHÜLER: | Aber warum denn? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgaben:
(1) Erläutere, weshalb der SCHÜLER so erstaunt ist.
(2) Beweise den Zusammenhang durch eine stichwortartig kommentierte Rechnung.
(3) Beschreibe den festgestellten Zusammenhang durch eine möglichst allgemeine Formel!
Klasse 10/4 : Den Begriff "Binomialkoeffizient" erklären
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir betreiben Kombinatorik und haben jetzt das Urnenmodell „Ohne Reihenfolge / Ohne Zurücklegen“ behandelt. |
SENSEI: | Dann weißt du sicherlich, wie viele Mög-lichkeiten es gibt, diesbezüglich aus fünf Objekten zwei auszuwählen? |
SCHÜLER: | Klar, das ist dann der Binominalkoeffi-zient „5 über 3“, also genau 5! geteilt durch 3! und (5-2)!=3!, also zehn. |
SENSEI: | Richtig gerechnet, aber es heißt „Binomialkoeffizient“, ohne „n“ in der Mitte. Hast du eine Idee, wo dieser Begriff herkommen könnte? |
SCHÜLER: | Nee, mit „Binomi“ verbinde ich nur die Binomischen Formeln. Und ich weiß, dass ein Koeffizient eine Zahl ist, die vor einem Term steht. |
SENSEI: | Genau. Was passiert denn, wenn du z.B. (a+b)^5 rechnen willst? |
SCHÜLER: | Naja, dann muss ich halt jeden Term jeder Klammer mit jedem Term der anderen Klammern multiplizieren und dann gleiches zusammenfassen. |
SENSEI: | Genau. Dabei erhälst du dann jeweils eine Anzahl von Termen a^5, a^4*b, a^3*b^2, a^2*b^3, a*b^4, b^5.Wie oft kommt denn dabei der Term a^3*b^2 vor? |
SCHÜLER: | Das müsste ich jetzt ausrechnen, wird eine lange, langweilige Rechnung. |
SENSEI: | Nein, das ist ganz einfach. Er kommt zehnmal vor! |
SCHÜLER: | Aber wie hast du das so schnell berechnet? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |
Aufgabe:
(1) Begründe, warum ohne umständliches Klammernausrechnen und Zusammenfassen bestimmt werden kann, dass der Term a^3*b^2 beim Ausmultiplizieren von (a+b)5^ genau zehnmal vorkommt.
(2) Erläutere, woher der Binomialkoeffizient "n über k" seinen Namen hat.
Klasse 10/5 : Wahrscheinlichkeiten untersuchen
SENSEI: | Was behandelt ihr gerade im schönen Fach Mathematik? |
SCHÜLER: | Wir beschäftigen uns mit der Wahr-scheinlichkeitsrechnung. |
SENSEI: | Wahrscheinlichkeit ist ein spannendes Thema. Aber schon Blaire PASCAL, der Begründer der Wahrscheinlichkeits-rechnung hat gesagt: „Alles, was nur wahrscheinlich ist, ist wahrscheinlich falsch!“ Also wozu braucht man dann ei-gentlich Wahrscheinlichkeitsrechnung? |
SCHÜLER: | Na weil man schließlich vorhersagen will, was wahrscheinlich passie-ren wird, wenn man es nicht genau vorhersagen kann … |
SENSEI: | Kann man das denn überhaupt? Schaue dir diese Münze an. Auf einer Seite ist eine Zahl, auf der anderen ein Adler. Auf welcher Seite wird sie liegenbleiben, wenn ich sie im Bogen auf den Boden werfe? |
SCHÜLER: | Das kann man natürlich überhaupt nicht sagen, die Wahrscheinlichkeit ist doch für beide Seiten gleich groß, oder? |
SENSEI: | (lacht) Nun, vielleich fällt dir die Prognose leichter, wenn ich dir sage, dass bei den letzten fünf Würfen der Münze jeweils der Adler oben lag, vielleicht weil der Adler fliegen kann? |
SCHÜLER: | Na das ganz bestimmt nicht! |
SENSEI: | Aber was wird denn wahrscheinlich passieren, wenn ich jetzt die Münze werfe? |
SCHÜLER: | Dann wird höchstwahrscheinlich die Zahl oben liegen, dass muss doch nun endlich mal passieren. |
SENSEI: | Das, lieber Schüler, war die schlechteste aller möglichen Antworten. |
SCHÜLER: | Aber warum denn? |
SENSEI: | Nun, genau das ist heute meine Frage an dich ... |